II. THE MATHEMATICAL SCIENCES:
THEIR STRUCTURE AND CONTRIBUTIONS

The mathematical sciences are the most abstract of the sciences, as suggested in Table 1.

 Field                             The Study of
 
 Mathematical sciences             Patterns, structures, the modeling of reality
 Physics                           Energy, matter, time
 Chemistry                         Molecules
 Biology                           Life
 Materials science                 Materials, structures
 Earth sciences                    The earth: continents, oceans, the atmosphere
 Astronomy                         Origin and evolution of planets, stars, and 
                                   the universe

The mathematical sciences have two major aspects. The first and more abstract aspect can be described as the study of structures, patterns, and the structural harmony of patterns. The search for symmetries and regularities in the structure of abstract patterns lies at the core of pure mathematics. These searches usually have the objective of understanding abstract concepts, but frequently they have significant practical and theoretical impact on other fields as well. For example, integral geometry underlies the development of x-ray tomography (the CAT scan), the arithmetic over prime numbers leads to generation of perfect codes for secure transmission of data on the Internet, and infinite dimensional representations of groups enable the design of large, economically efficient networks of high connectivity in telecommunications.

The second aspect of mathematical science is motivated by the desire to model events or systems which occur in the world — usually the physical, biological, and business worlds. This aspect involves three steps:

• Creating a well-defined model of a real situation, which itself is frequently not well defined. Such modeling involves compromises between the need for the model to be faithful to the real situation and the need for it to be mathematically tractable. An appropriate compromise usually requires the collaboration of an expert on the subject area and an expert on the mathematics.

• Solving the model, through analytic or computational means or a mixture of both.

• Developing general tools, which are likely to be repeatedly useful in solving particular models.

Examples of mathematical modeling include the quantum computer project, DNA-based molecular design, pattern formation in biology, and the fast Fourier transform and multiple algorithms used daily by engineers for numerical computation.

The mathematical sciences are disciplines in themselves, with their own internal vitality and need for nourishment. But they also serve as the fundamental tools and language for science, engineering, industry, management, and finance. They are inextricably linked to these "user" fields and they frequently draw inspiration from them. The mathematical sciences represent a mode of thought based on abstraction that sustains precision and permits careful analysis and explicit calculation. Thus mathematics has a dual nature: it is both an independent discipline valued for precision and intrinsic beauty, and it is a rich source of tools for the world of applications. Mathematics might be described as having abstractness internally and effectiveness externally.

The two parts of this duality are intimately connected. The search for order, symmetries, and regularities in patterns is the heart of research in pure mathematics. Results of this research are very durable, sometimes finding important application in unexpected ways decades after their discovery. A major reason for this is that results in mathematics, once proven, are never disproved -- even though they may be superceded by more powerful results. Other sciences, by contrast, move towards truth by a process of successive approximations.

In the United States, mathematics research, which is carried out principally at universities, may be segmented (somewhat arbitrarily) into nine sub-fields, as described in Table 2.:

 Subfield                          The Study of
 
 Foundations                       Logical underpinnings of mathematics
 Algebra and Combinatorics         Structures, discreteness
 Number Theory and Algebraic       Properties of numbers and polynomials
  Geometry
 Topology and Geometry             Spatial structures, patterns,shapes
 Analysis                          Extensions and generalizations of the calculus
 Probability                       Randomness and indeterminate phenomena
 Applied Mathematics               Problems arising in nature
 Computational Mathematics         Problems whose solution uses the computer
 Statistics                        Analysis of data

The boundaries between these subfields are neither fixed not solid, and some of the most interesting and fruitful developments in mathematics come at the interfaces of subfields. Some areas of research appear in more than one of these categories; e.g., for example, Theoretical/Mathematical Physics appears in Topology/Geometry, Analysis, and Applied Mathematics.

The Mathematical Sciences Research Community

The mathematical sciences research community differs from other research communities in several ways. Mathematical research is the epitome of "small" science; that is, much research is done by individuals working alone, with modest equipment needs such as workstations. (Increasingly, however, some mathematicians need access to supercomputers and visualization labs.) Also, mathematical research is long-lasting, and rich in references to older literature, so that mathematicians are more dependent than other scientists on good libraries. Finally, mathematicians are more closely associated with teaching and with educational institutions than other scientists. Most research mathematicians are university based, so that their culture has an academic orientation.

In 1995(see Endnote 5), approximately 16,000 (over 65%) of the doctoral mathematical scientists in the United States were located at institutions of higher education. Of these, 6,427 worked at doctorate-granting institutions and represent the heart of the U.S. academic research community. Less than 25% of doctoral mathematicians were employed in private industry, and 4.2% were employed in government. Of the 1994-95 cohort of U.S. doctorate recipients, more than 50% anticipated faculty positions at educational institutions, with an additional 25% planning U.S. postdoctoral appointments, presumably as a precursor to academic careers.

Mathematical scientists in industry seldom carry the title "mathematician;" they are usually known as "engineers," "systems analysts," or by other titles, (see SIAM report)(see Endnote 6). Thus they lack the mathematical identity and consciousness of their academic counterparts and in contrast to chemists and engineers, tend to be poorly connected to the university community.

Mathematical Sciences as an International Discipline

Both by its abstract nature and by convention, mathematics knows neither linguistic nor political boundaries. Its language is usually decipherable from equations and relations alone; when words are needed, mathematicians around the world use English by common agreement -- just as scholars once used Latin. In the same spirit, mathematicians have managed to transcend political differences and borders, even during the Cold War. And because mathematicians do not require specialized laboratories to conduct their research, they travel freely between universities and between countries. The result of these customs and agreements is that mathematics is an extraordinarily open and international activity.

The number of highly active research mathematical scientists worldwide is small —probably well under 10,000 — so that a given subarea may be populated by only a tiny number of highly specialized individuals. They know each other well regardless of their country of residence; share a common, specialized vocabulary; and collaborate extensively even over long distances. Mathematical science conferences typically host participants from many countries; meeting one’s peers is essential for the exchange of ideas which may not appear in published work.

Because of this international culture, mathematicians frequently take up sequential residencies in different countries or alternate between countries. The United States, with its commitment to freedom, a high standard of living, and excellent universities, has benefited enormously from flows of foreign-born mathematicians; in the same spirit, Americans serve on mathematical science faculties in almost every country in Europe. For these reasons, local changes in the support of the mathematical sciences in any country can result in the rapid migration of mathematicians, such as the great emigrations from Europe before World War II and the former Soviet Union at the end of the Cold War.

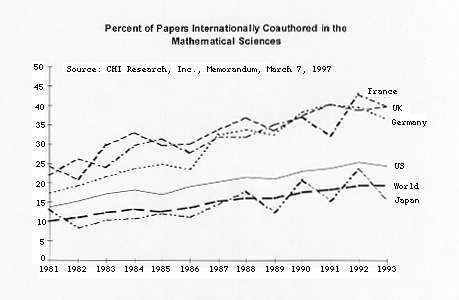
Mathematicians also collaborate internationally on research, a trend that has been growing consistently for nearly two decades. The number of papers co-authored by mathematicians in the five major mathematical nations (see Endnote 7) with researchers in other countries rose about 50% between 1981 and 1993, and this tendency continues.

The growth in co-authored papers by researchers in the United Kingdom, France, and Germany reflects the growing unification of the countries in the European Union.

Mathematics students tend to gather in the strongest research centers, a tradition that began over a century ago. Before 1940, it was common for the best U.S. students to study in Europe; after World War II, the U.S. reputation in mathematics grew rapidly, and for the past 15 years, a majority of Ph.D. graduates of U.S. institutions have been non-U.S. citizens. In 1996, non-U.S. citizens earned 55% of total doctoral degrees in mathematical and computer sciences(see Endnote 8). Other strong international research centers are also attracting foreign students. In France, international students now earn one out of three doctoral degrees awarded in all fields of science; in Japan, that proportion is 40%; and in England, 27%, with many students from commonwealth countries and the United States(see Endnote 9). Germany supports foreign graduate students and postdoctorates on Humboldt Fellowships.

The Role of Mathematics in Society

Although most of the mathematical research community is university-based, the impact of mathematics on society is pervasive. Mathematics underpins most current scientific and technological activities. Whole new areas of mathematics are evolving in response to problems in experimental science (biology, chemistry, geophysics, medical science), in government (defense, security), and in business (industry, technology, manufacturing, services, finance). All of these areas now require the analysis and management of huge amounts of loosely structured data, and all need mathematical models to simulate phenomena and make predictions. Modeling and simulation are essential to fields where observable data are scarce or involve a great deal of uncertainty, such as astronomy, climatology, and public policy analysis. Addressing such complex problems calls for openness to all of mathematics and to the emergence of new mathematics. Progress requires radical theoretical ideas as well as significantly greater collaboration between pure mathematicians, statisticians, computer scientists, and experimental scientists.

The applications of mathematics in the future will require closer partnerships between mathematical scientists and the broader universe of scientists and engineers. Meeting the complexity of tomorrow’s challenges will demand insights across the full spectrum of the mathematical sciences. Both the theoretical and the industrial impact of this development will be enormous. Table 3 illustrates some of the present and potential contributions of mathematics to society.

The sciences have always used mathematics to formulate theory and underpin simulation and statistics to design productive experiments. Wherever numbers or symbols are manipulated, the manipulations rest on mathematical relationships. With the advent of high-speed computers and sensors, some experimental sciences can now generate enormous volumes of data --- the human genome project is an example -- and the new tools needed to organize this data and extract significant information from it will depend on the mathematical sciences. Hence the mathematical sciences are now essential to all three aspects of science: observation, theory, and simulation.

The following examples illustrate ways in which mathematics contribute to areas of broad concern to our nation:

National security. The security of complex communications systems--voice, data, and electronic--rests on mathematically sophisticated tools. Stockpile stewardship--the maintenance of the nuclear arsenal without testing--will be based on mathematical modeling and advanced computation. The operation of national surveillance systems requires extensive use of mathematics for collection and analysis of data. Military systems are being transformed by the application of mathematical-based systems for intelligence, logistics, and warfighting.

Technology. Mathematics is ubiquitous in the design, manufacturing, and use of technology. No complex system--from microprocessors to aircraft engines, from satellite communications networks to home marketing systems, and from the air traffic control system to the laptop computer--could exist without the application of mathematics.

Education. The role of mathematics in educating the work force is crucial for the well-being of the nation. Scientists and engineers depend on the mathematical sciences and need a sound foundation in that discipline to succeed. For the average citizen, a grounding in mathematics, at least through the secondary level, is essential to modern citizenship. Innumeracy is as crippling as illiteracy.

Medicine. The operation of modern medical imaging systems--CAT scanners, nuclear imagers, Magnetic Resonance Imaging (MRI)--depends on the mathematical processing of signals. The success of the human genome project will require the use of mathematics to search for information that correlates genetic sequences to human disease. Elucidating the complex geometry of protein folding is the key to understanding protein functions. The management of hospital patient records will increasingly require the application of mathematics to construct efficient databases.

Finance. Mathematics has become indispensable in measuring risk and modeling the behavior of financial instruments, financial institutions, and financial systems (individual countries, trading blocs, and global systems, such as international settlements). The combination of probability theory and advanced financial models with increased data, capacity, algorithm efficiency, and computational speed facilitates the sophisticated modeling of interest rates, currencies, commodities, equities, and other financial instruments. Better understanding of areas such as value at risk, portfolio theory for credit exposures, and non-linear instruments depends on the application of mathematics.

Environmental monitoring. Building useful models of oceans and atmospheres to predict the impact of human activities on the environment is essential to the formulation of sound public and regulatory policies. Climate models require the manipulation of massive quantities of data and the study of complex simultaneous interactions (for example, among the many trace chemicals in the atmosphere). All such models are based on uncertainty; to judge their validity will require heavy use of mathematics.

In broad terms, both the techniques of the sciences and the needs of society are dramatically more complex than those of the past. The ability to understand new needs and systems, and to predict and control their behavior, will require two elements: i) new mathematical ideas and methods, and ii) more effective collaboration between all groups actively concerned with them -- disciplinary scientists, engineers, computer scientists, and members of relevant professions, from medicine to public policy.